As the consumer electronics devices in today’s world become smaller and smaller, the available space for magnets in these devices is becoming more limited. To ensure the device’s overall dimensional requirements, Neodymium magnets (NdFeB) in today’s electronics are typically smaller than 1mm in thickness. In some cases, these magnets can be as small as 0.2mm thick.
If the magnet designer wants more magnetic force with the given dimensions, they sometimes have the option to increase the grade of magnet. When we look at the table of NdFeB magnets, a higher grade of magnet has higher remanence field (Br). For example, N52 magnets have a Br = 1.42T and N35 only have a Br = 1.17T. On paper N52 magnets should have much stronger force than the N35 right? But designers find that the difference between these two grades is much smaller than expected, especially on very thin magnets (in the axis of anisotropy). How do we select the right grade and what role of magnet dimensions play in it?
Permeance coefficient (Pc) is the ratio between flux density (Bd) to magnetic field strength (Hd) at the operating slope of the B-H curve of a certain magnet. It is independent from material and only related to the dimensions of the magnet. The equation for Pc is based on magnet shape and can also be calculated by FEA. If a magnet is magnetized through the thickness (axis of anisotropy), the thicker the magnet, the higher the Pc value is. For example, a 5x5x5mm magnet, shown in the figure below, has a Pc = 2.15, and a 5x5x0.2mm magnet only has a Pc = 0.14.
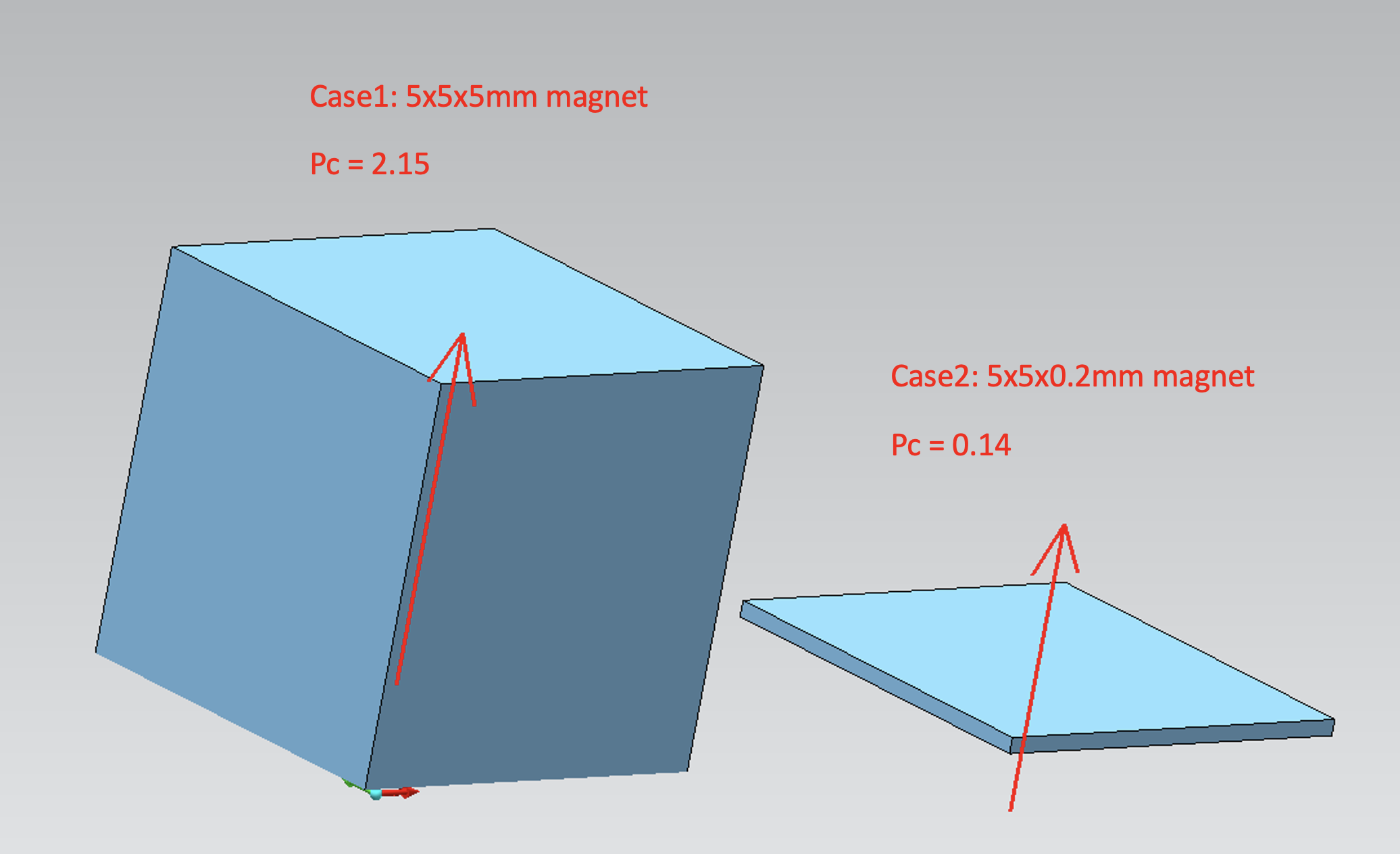
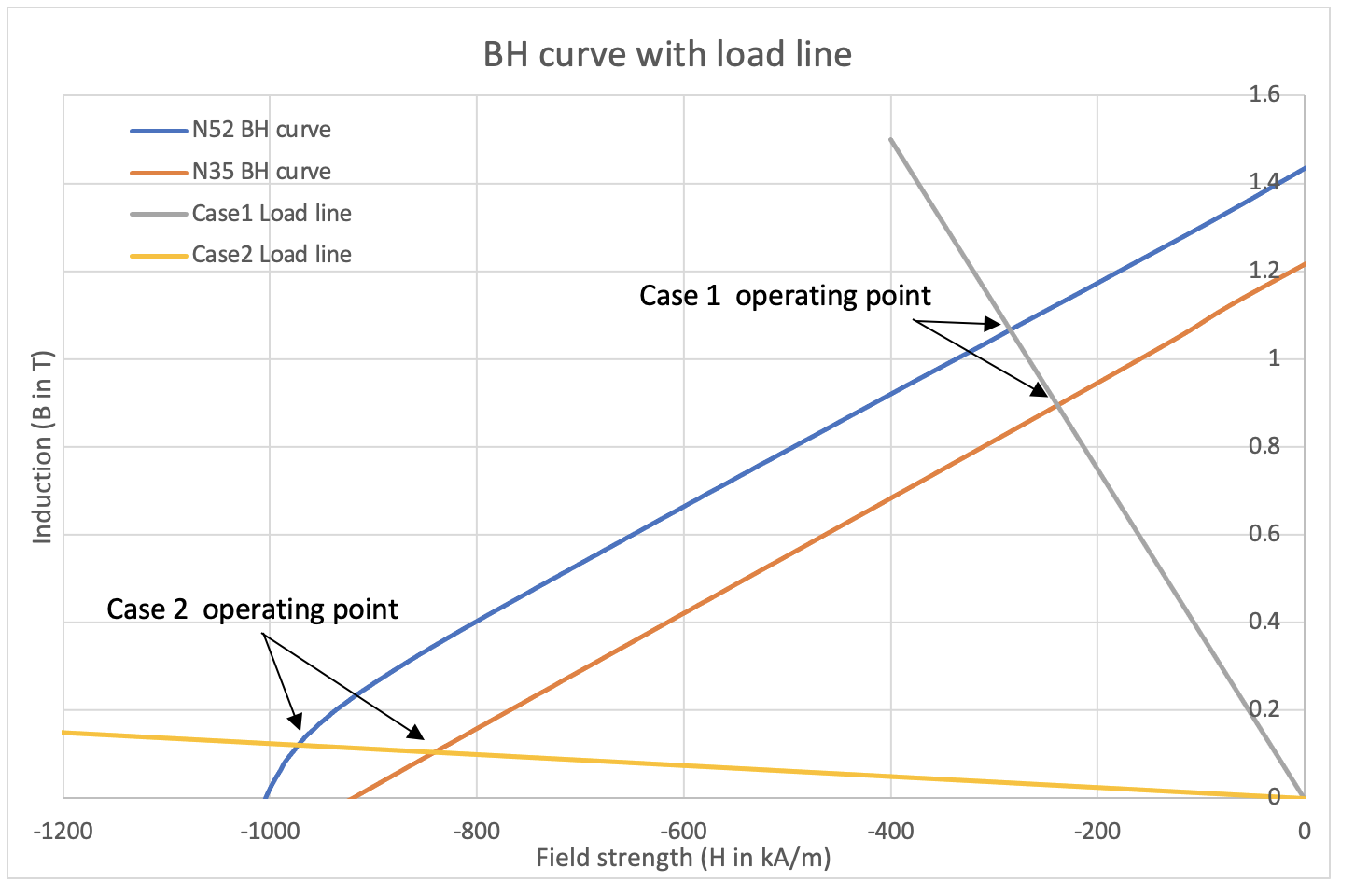
On the B-H curve, the Pc value effectively describes how the dimension of magnets affect the operating performance of the magnet. If we draw a line from the original point and use the Pc as the slope (the load line). The intersection point with the BH curve is the actual operating point of this specific dimension/grade of magnet.
If we use two different grades (N35 and N52) on Case1 and 2 introduced above. We will notice that for Case1 where the magnet is thick enough and has high Pc value (2.15), the operating magnetic induction for both grades is high and close to the remanence field. Meaning the magnet is still strong enough. Also, the difference of magnetic induction between N35 and N52 is significant as the load line slope is steep. Which indicates that increasing the grade will give us a high increase of magnet strength. However, for Case2 where the magnet is thin and has very low Pc value (0.14), the operating magnetic induction becomes so low (Y-Axis) that the magnet loses most of its strength. Also, as the load line becomes flat there is no effective difference between N35 and N52. Thus, increasing the grade will no longer help us increase the force.
As a result, if we attach both case magnets to a steel shunt and change the magnet grade, we can measure the force they provide. The table below showcases the force in Newtons for both N52 and N35 grades in the two different cases mentioned:

From the table, it is evident that for the 5x5x5mm magnet, the N52 grade magnet provides a force that is 1.43 times that of the N35, which is a substantial increase. This indicates that for thicker magnets with a high Pc value, opting for a higher-grade magnet like N52 does indeed result in a significantly stronger magnetic force.
On the other hand, when we look at the 5x5x0.2mm magnet, the forces provided by both N52 and N35 grade magnets are nearly identical. The ratio of their forces is essentially 1, suggesting that there is no noticeable benefit in selecting a higher-grade magnet when dealing with ultra-thin magnets.
This observation highlights a crucial point in the design of magnetic applications in consumer electronics; the importance of considering the dimension of the magnet, specifically its thickness, when selecting the grade of the magnet. While a higher-grade magnet typically implies a stronger magnetic field, this advantage diminishes as the magnet becomes thinner.
Therefore, designers must weigh the costs and benefits when choosing the grade of the magnet for their application. For applications where the magnet can be made thicker, it may be worth investing in a higher-grade magnet. However, for ultra-thin applications, the additional cost of a higher-grade magnet may not justify the negligible increase in magnetic force.
In conclusion, the permeance coefficient (Pc) is a critical factor in the performance of a magnet. By understanding and applying the concepts of the Pc and the B-H curve, designers can make more informed decisions about the grade of magnet needed for their specific application, ensuring optimal performance without unnecessary expenditure. Contact Quadrant to learn more.
